H1 Your Exams with Our Specialised Courses and Grinds


With H1Maths, YOU take full control of your learning journey.
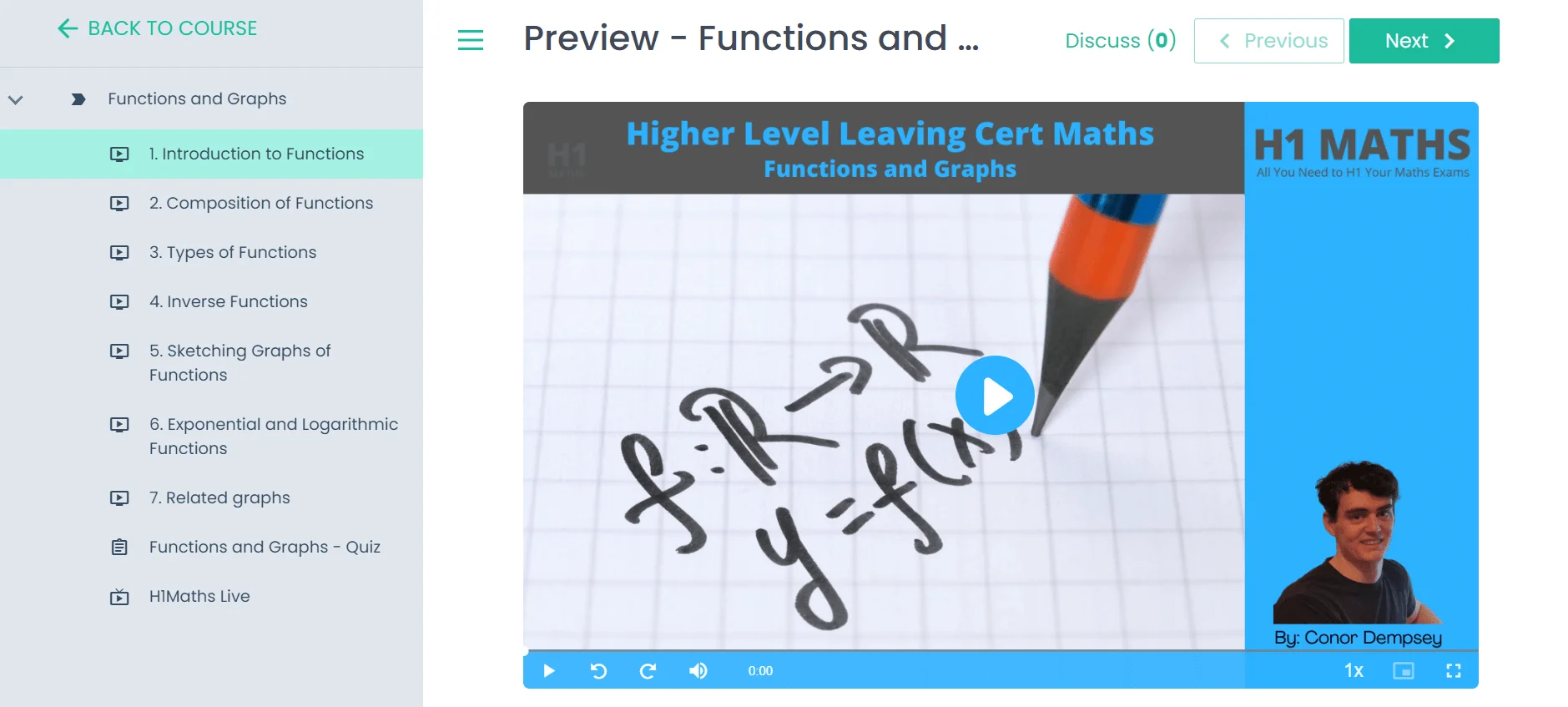
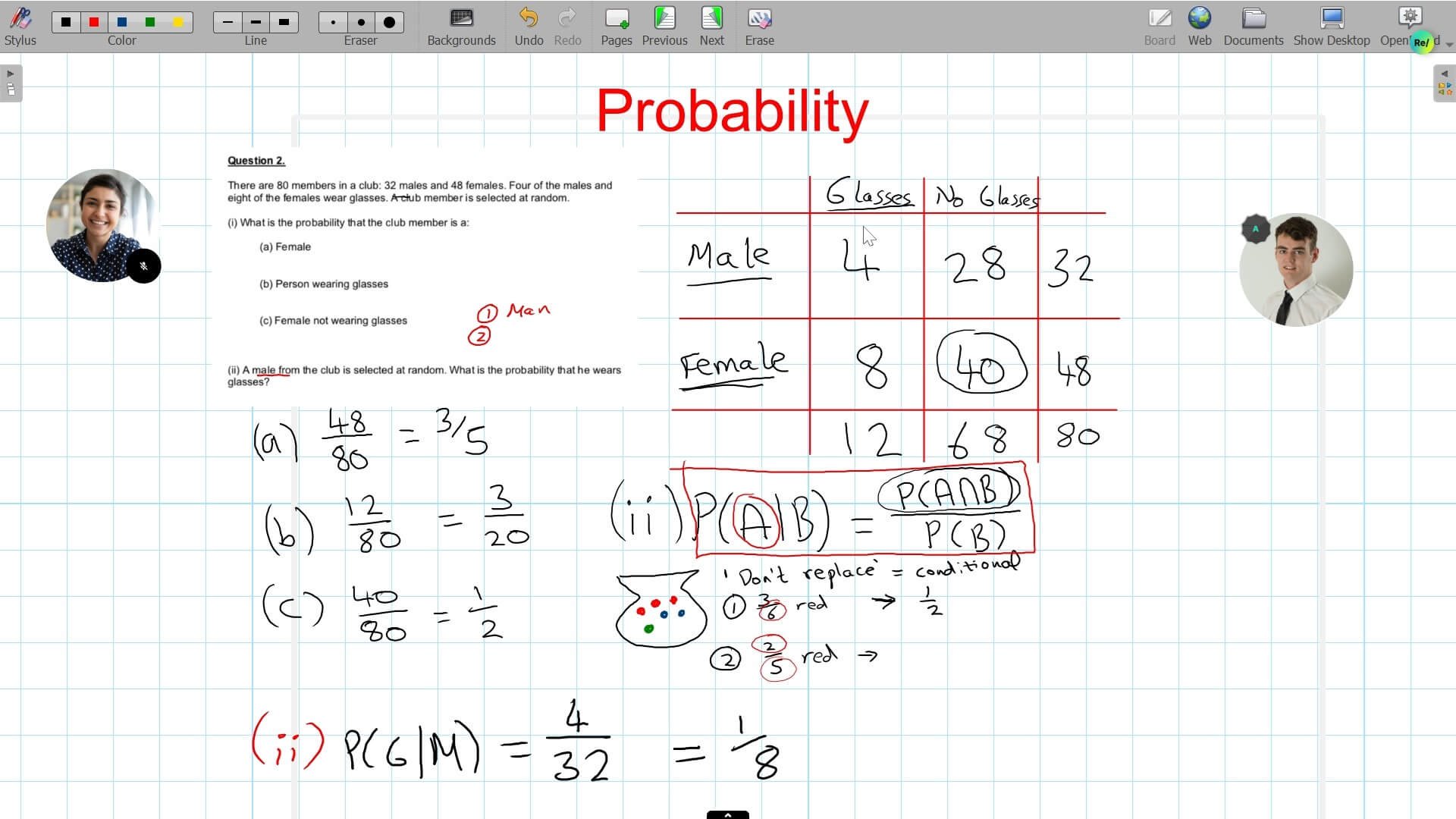
Are you a night owl or an early bird? With H1Maths, you gain unlimited access to 50+ hours of on-demand lessons that you can watch whenever, wherever, and as many times as you want.
Complete quizzes on every topic to assess your learning progress and receive personalized feedback from our expert instructors to guide you on your journey to H1 success.
What you get with a H1Maths subscription

The Best Value On Online Irish Maths Courses



Hear from those that have benefited from using H1Maths

H1Maths has helped me study better. I found the end-of-topic quizzes to be very helpful for revision.

The additional assignments and one-to-one tutoring were exactly what I needed coming closer to the exams.

Being able to look at pre-recorded lessons on my own time allows me to spend more time in the classroom listening and learning.

The exam paper solution videos have helped me see patterns in the wording of questions. I'm a lot more confident now!
Please check your inbox for 10% off your next grind. (Don't forget to check your promotions!)
Our excellent customer support team is ready to help.